Main point: Let an adversary add realistic data to your analysis to see if it is resilient.
At the heart of statistics is the desire to make what we could call question / answer equilibrium. The question has a sound relation to that answer via the observation. The observations should ideally be monotonically increasing but ever true and the question / answer congruence should be resilient to additions to the data. This requires us to be careful about the questions in particular and sometimes we need to amend the question to make the answer more resilient.
Imagine a question like "what is the life expectancy". We can calculate that by taking the mean of all ages of all deceased people we have registered and report that as the answer. However, this is not resilient as new data might alter the answer because people get older. To mitigate this we can reiterate on the question and ask "what is the life expectancy in 2020" which would have the resilience to new data.
A formal method is to apply an adversarial model to statistics. To do this we make a system where we can prove that the addition of new data will change the question / answer relation. A such formalism can be based on typed graphs where we model all that entities and their relations. We prove that adding new entities will not change already published results.
We can imagine a system that has the following entities:
Person, Country, Year. These entities can be linked by
Person -- livesIn --> Country, Person -- deceasedIn --> Year. An example
dataset to adhere to that ontology could be laid out as follows
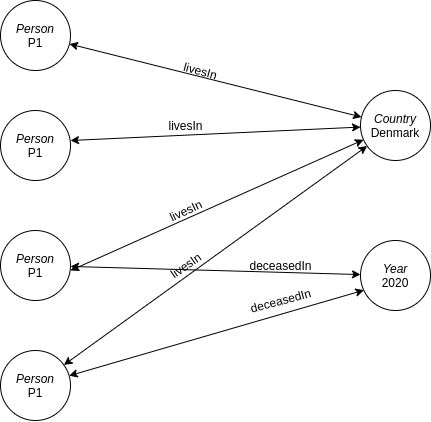
To answer questions in the above-pictured dataset we can use the Monte Carlo simulation technique.
For the first question, "what is the life expectancy," we draw a deceased person
10.000 times and average their ages. To answer the other question,
"what is the life expectancy in 2020" we draw a person that has a deceasedIn
relation to 2020 10.000 times and average over their ages.
For each of the questions, we invite the meanest adversary we know and allow her to put in new entities with one rule: The entities are realistic. Ie. as we are in 2021 now it is not possible to add more people deceased in 2020. The adversary quickly figures out that she can merely decease one of the still-alive people to change the answer to the first question. However, for the second question no new relations within the specified scope would
The above network would obviously be wildly bigger in reality and also include many more classes of data. Data might be gathered from several different data sources which can be modeled using multi-layer networks. Furthermore, When communicating in real life one should also take context into account. Ie. If we ask "what is the life expectancy" it can reasonably be assumed that it is in the year 2020 (and not eg. 1820).
I am currently building Fog that is a Haskell library to experiment with formalisms for skeptic reasoning. If you are also curious about this field and want to talk, please reach out!